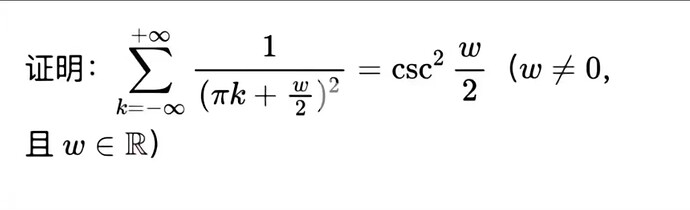还有就是美女和小孩的模型较多，历经沧桑的模型很少。我打入：“月亮在白莲花般的云彩里穿行，晚风吹来一阵阵快乐的歌声，我们坐在高高的谷堆旁边，听妈妈讲那过去的事情。。。”得到的是这样的画面：
我修改提示词，说，妈妈是短发，中年人，结果就改成这样的了：
大概AI不懂，月亮下讲故事也可以是悲沧的旧事。想了一想，就让AI给我画面无表情，带着小黑猫坐墙根的流浪汉，AI果然把握得很准：
提示语设定是这样的：
在Bing上面也试了，回馈也不算太差：
我说在多伦多的queen街，就给我换成了一条狗，大概AI在queen街上，只见过带狗的流浪汉，没见过带猫的：
所以，AI说到底，还是只能做它熟悉的事——也就是简单追循模型训练的方向。没有更多的training，AI能做的事非常有限；training做到位了，AI的表达力的确爆棚（AI不知道，多伦多的大街上，是不能摆放一瓶酒的，流浪汉也不行）。
现在发布的SD3模型是medium版本，据说以后还要发布一个Large版本，训练参数达到80亿，是现在的一倍。或许有些改进。
现在只是AI的开端，以后肯定会越来越厉害。
我会时不时地玩玩，让自己不要太早落伍。
这就说明证明过程没问题。我才国内把这个封了，是不希望学生上网抄这一类的答案吧。
我也用GPT3.5试过，3.5不懂得原式的image。3.5虽然也可以证明，但很难读懂证明过程：
To prove the given equation:
[
\sum_{k=-\infty}^{+\infty} \frac{1}{(\pi k + \frac{w}{2})^2} = \csc^2 \frac{w}{2} \quad \text{for} \quad w \in \mathbb{R}, ; w \neq 0,
]
we can use the theory of complex analysis, specifically the residue theorem and properties of the cotangent function. Here’s a detailed proof:
Consider the function:
[
f(z) = \cot \left( \frac{z}{2} \right)
]
This function has poles at ( z = 2\pi k ) for ( k \in \mathbb{Z} ).
For a meromorphic function ( g(z) ), if ( z_0, z_1, z_2, \ldots ) are its zeros (counting multiplicities), and assuming ( g(z) ) has simple zeros, the sum of the reciprocals of the squares of the zeros can be written in terms of the residues of the derivative of ( \frac{1}{g(z)} ). This idea is grounded in the Mittag-Leffler theorem.
For ( \cot(z/2) ), the zeros are at ( z = 2n\pi ) and the poles are at ( z = (2n+1)\pi ). We have:
[
\frac{\cot(z/2)}{(\pi k + \frac{w}{2})^2}
]
To apply the Mittag-Leffler theorem, consider the function ( g(z) = \sin(z) ). The zeros are at ( z = n\pi ) and the residues of ( \cot(z) ) at ( z = k\pi ) are given by the standard residue of ( \cot(z) ).
The sum:
[
\sum_{k=-\infty}^{+\infty} \frac{1}{(\pi k + \frac{w}{2})^2}
]
corresponds to the residues of the function ( \cot(z/2) ) at the points ( z = \pi k + \frac{w}{2} ).
Using known results from complex analysis and the properties of the cotangent function, the sum of squares of the reciprocals of the shifted arguments of the cotangent function is:
[
\sum_{k=-\infty}^{+\infty} \frac{1}{(\pi k + \frac{w}{2})^2} = \csc^2 \frac{w}{2}
]
Thus, the proof is completed by recognizing the standard result from the theory of residues and the properties of the cotangent function, establishing the given identity:
[
\boxed{\sum_{k=-\infty}^{+\infty} \frac{1}{(\pi k + \frac{w}{2})^2} = \csc^2 \frac{w}{2} \quad \text{for} \quad w \in \mathbb{R}, ; w \neq 0}
对于放烟花，多伦多人还是蛮自觉地，不会太离谱。当然，当局也没管得那么死，差不多就行了。
按照规定，只能在7月1日当太可以燃放，前一晚是违规的；第二，规则明确说了，只能在自己私有的地域燃放，比如说前院，后院。不可以在住宅区车道上，也不能在停车场，更不能在大大小小未经特别批准的公园里燃放。实际上我家附近有个个社区的活动场，孩子们每年都聚集在那儿燃放。
社区活动场所应该是管不过来，再说了，孩子们也不会太过分，通常也就是很小的花炮玩一下。不过在大一点的公园，还真的有警察巡逻。
晴天，阳光照在湖面上，波光粼粼，碧水如随风摆动的锦缎，又如银光闪闪的明镜；蓝天白云倒映湖水中，湖就成了清澈的天，蹁跹的白鹭、游动的白鹅，不知道是在天上飞，还是在湖里游。雨天，最好是细雨霏霏，眼前的湖面澹澹兮生烟，远处的青山如黛，戴一顶斗笠，披一身蓑衣，撑一叶扁舟，向清水深处漫溯……
----------------节选自： 山水之间（散文）， 董华
SDXL版
网上有人说， SD3 最擅长文字的描绘，描绘的越详细，其画出来的图就越逼真。比试比试看看。
SD3 版
比较一下，看起来SD3的图片更接近提示词。
直接引用原文有点小问题，场景在流动而不是定格唯一。先说的场面是阳光和粼粼波光，后说的是天空转阴并有细雨，所以AI的确不容易处理。
以后如果有普及性的短片生成软件，这种流动场景的画面，也很难生成的——除非有人愿意花大功夫去训练模型。
毕竟西湖六月中，风光不与四时同。
接天莲叶无穷碧，映日荷花别样红。
What is West Lake in June the day scenery,
The scenery and the other seasons are different.
Lotus leaf by God as a green,
The sun is bright red lotus。
译文
六月里西湖的风光景色到底和其他时节的不一样：
那密密层层的荷叶铺展开去，与蓝天相连接，一片无边无际的青翠碧绿；
那亭亭玉立的荷花绽蕾盛开，在阳光辉映下，显得格外的鲜艳娇红。
AI 圖?
颂英雄精忠碧血衷肠，
诉名士倜傥千古吟咏，
叹才女痴情一瓣心香。
小说绣像起源于杭州。明代主要是简单地描画人物，后来慢慢把人物放置于景物之中。
清代末期传到上海，才出现大量以风景为主人物为辅的“绣像”，偶尔，还有只有风景没有人物的绣像。绣像的本意，就是画笔人物写生，绣像用来画风景，虽然不多见，却也新颖。
小时候，看过一本民国初年刊印的1830年代的著名的科幻小说《80天环游世界》的绣像本，画得很传神。其实，民国初年已经有连环画，但连环画的绘图方式都是西洋风格的，和明代发展起来的绣像风格相差太远。
给我印象最深的是清末明初，给当时的一个科幻故事画的绣像，以地球人殖民月球为主题的一个故事集，故事的内容不仅有科幻的，也有现实中，十里洋场中国人被歧视被欺负的章节：
故事中说用美洲人（美国人）的热气球往来月球。要是真的用热气球就可以了，那该多好啊，美国俩老人受困在太空的问题就很容易解决了。
前几天，路边一青年对一老翁说几句话。
听了后。
一、
打关键词 - 登陆月球 – 搜寻，
第一页，没中国登陆月球。
第二页，没中国登陆月球。
第三页，没中国登陆月球。
页面显示到第六页，
中国载人月球探测工程登月阶段任务最新进展情况公布
紫荆杂志
2024年4月24日 — 长征十号运载火箭、梦舟载人飞船、揽月月面着陆器、登月服等主要飞行产品均已完成方案研制工作，正在全面开展初样产品生产和各项试验。飞船、着陆器已基本 .
二、
页面显示到第七页，
台湾首次登陆月球！中央大学「深太空辐射探测仪」、第4季将 …
NOWnews今日新闻
2024年1月29日 — 1969年「阿波罗计划」成功登陆月球，开启人类登月的伟大梦想，近几年世界各国积极展开「重返月球」任务，台湾在国立中央大学的主导下，2024年将展开 …
三、
打关键词 - 登陆月球 加字 (挖土) – 搜寻，页面显示到第一页，
到月球背面去「挖土」
新华澳报
1 天前 — 2024年6月4日7时38分，嫦娥六号上升器携带月球样品自月球背面起飞。上升器先后经历垂直上升、姿态调整和轨道射入三个阶段，成功进入预定环月飞行轨道 …
嫦娥六号登月倒计时：48小时完成“挖土”！返航时间确定，外媒
手机网易网
2024年5月28日 — 按照计划，嫦娥六号任务将会持续大约53天时间，从5月3日发射升空，至今已经飞行了20多天时间，预计在6月2日左右登陆月球，然后花48小时来“挖土”，预计在6 .
看一讀者留言:
您知不知道: 為什麼民進黨要發橙色警告台灣人最好不要去大陸旅遊 ?
一位台商朋友這樣說: 因為民進黨害怕台灣人去大陸後，看到聽到以下幾件事:
前几天，路边一青年对一老翁说:
你不要又说骗人的话了，大陆怎么可能?
大陆的飞弹火箭怎么可能，能射到台地。
大陆的火箭怎么可能，能射到月球挖了土，再回到地球。
梧葆老兄切切注意，不要和任何人争辩这些东西，争赢了又能如何。
我现在根本就不和任何人争辩。跟一个困守在信息茧房中的人争高低辩是非，是不会有任何效果的。
这里，如果直接引用“美人”，（beauty），不管怎么调整距离，它都给你一个真面美女肖像。这使AI对美女的理解，所以把美女去掉，换上girl，再加上距离，就可以画出接近意境的写意画来了。
100米远
500米远
女孩走得很远了，快看不见了
这个是Copilot Pro 画的？
是的。
现在，各路AI都在进步。copilot最大的问题是，很容易就画成韩国人或者日本人。
楓葉生活留言板 www.m9981.com
